Dearun软件操作
User Guide

软件简介
Dearun软件包含了当前DEA研究领域的主流模型,包括基础效率模型、超效率模型、网络DEA模型以及动态Malmquist指数分析,并可以处理存在非期望产出的情形。本文将向您介绍Dearun软件的使用流程,您可以通过下载文中的实例数据进行软件操作,便于您更快的上手本软件。
本页面的模型介绍与软件操作方法为之前的版本,已于2022年7月停止更新,且后续将不再更新!
所有帮助文件将全部内置在软件界面里,在软件中点击不同模型的帮助按钮即可获取更多支持,软件内的帮助会更加详细!!
Dearun功能介绍
恭喜您已经成功打开了Dearun,接下来将向您介绍这个软件的功能:
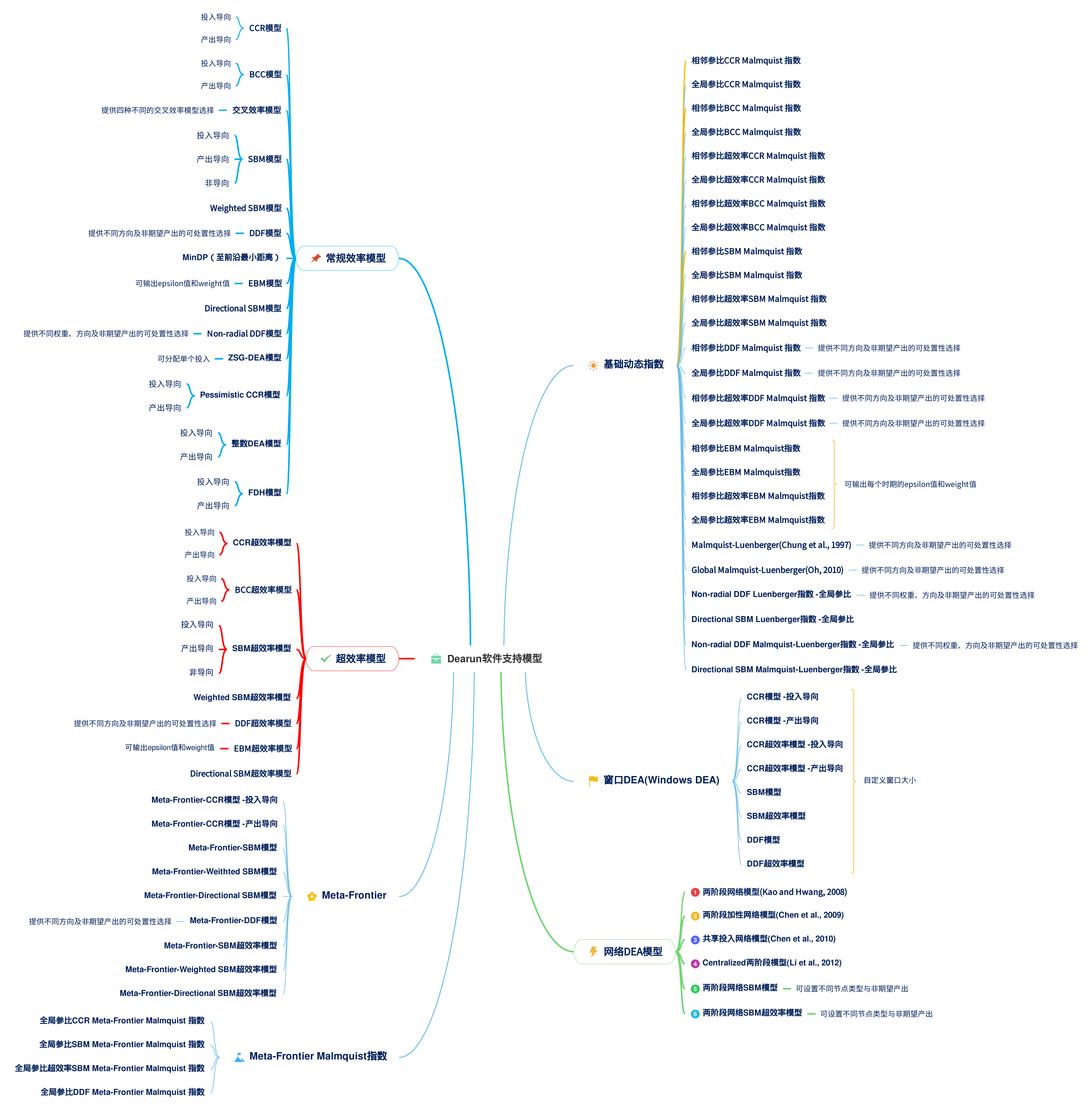
Dearun使用流程
基础效率模型与超效率模型
- 点击“导入表格”(参考实例数据),请注意表格的导入形式为:
DMU名称 投入 产出 非期望产出 DMU1 xxx xxx xxx … … … … DMUn xxx xxx xxx
数据格式检查
- 导入数据后,点击数据格式初步检查中的
截面选项,进行数据格式检查。
数据检查选项会对您导入的数据进行初步的检查,如是否包含0值、空值或非数值(有些同学在整理数据的时候,可能会出现一些excel的错误公式,从而产生非数值的情况,如:#VALUE!)
- 如数据没有上述情况,则有如下输出:
检查结果: 经过初步检查,数据内无空值、0或非数值的情况,请进一步选择模型进行计算。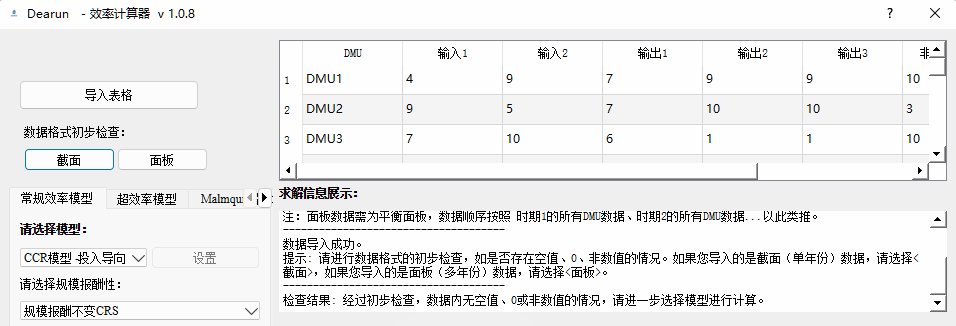
- 如数据存在上述情况,则有如下输出:
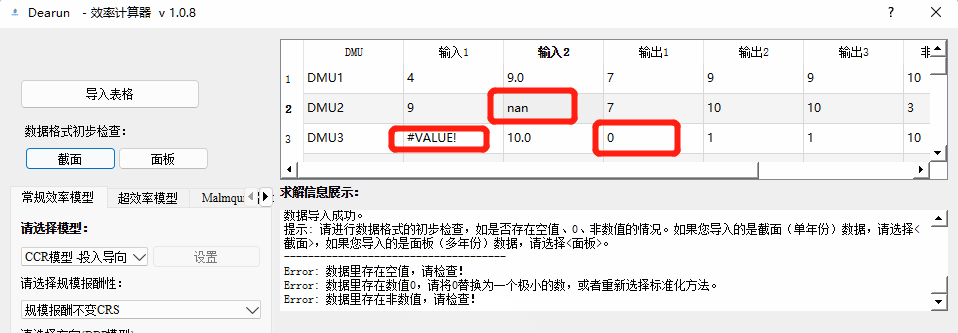
数据检查选项只会对数据进行初步的检查,没有问题不代表数据格式完全正确,请先保证您的数据是严格按照所需格式进行导入。模型选择及计算
- 正确导入表格后,会在右边栏出现表格内容
- 选择需要测算模型,默认CCR模型 -投入导向
- 选择规模报酬性,默认CRS
- 如果选择是DDF模型,请选择合适的方向;若选择的是CCR或SBM模型,“请选择方向”一栏默认即可
- 填写投入变量的个数,如果有2个投入,请填写阿拉伯数字“2”,不要写多余的字
- 填写产出变量的个数,同上
- 填写非期望产出变量的个数,同上,需注意无非期望产出的话,默认即可
- 点击“开始计算”,右边栏出现计算过程信息
- 最下面出现计算结果的表格,点击“结果保存”,结果将会储存在与你导入数据的同一个文件夹内
- 若测算超效率模型,步骤同上,需注意需要将选项卡切换到
超效率模型
操作演示
以SBM模型为例,数据同上,包含2个投入,3个期望产出,2个非期望产出:
动态效率模型(Malmquist指数)
- 切换选项卡为
Malmquist指数 - 点击“导入表格”(参考实例数据),请注意表格的导入形式为:
时期 DMU名称 投入 产出 非期望产出 period_1 DMU1 xxx xxx xxx … … … … … period_1 DMUn xxx xxx xxx … … … … … period_m DMU1 xxx xxx xxx … … … … … period_m DMUn xxx xxx xxx
- 请严格按照 时期、DMU名称、投入、产出、非期望产出 的顺序进行存放数据
- 数据纵向排列顺序为:period_1的截面数据、period_2的截面数据……
- 第一列放时期,第二列放DMU名称,第三列之后放指标数据
- 时期按照从小到大的顺序,如2019、2020、2021、2022
- 数据的形式与之前版本有一定的更改,以本格式为准
数据格式检查
- 导入数据后,点击数据格式初步检查中的
面板选项,进行数据格式检查。
数据检查选项会对您导入的数据进行初步的检查,如是否包含0值、空值或非数值(有些同学在整理数据的时候,可能会出现一些excel的错误公式,从而产生非数值的情况,如:#VALUE!)
- 如数据没有上述情况,则有如下输出:
检查结果: 经过初步检查,数据内无空值、0或非数值的情况,请进一步选择模型进行计算。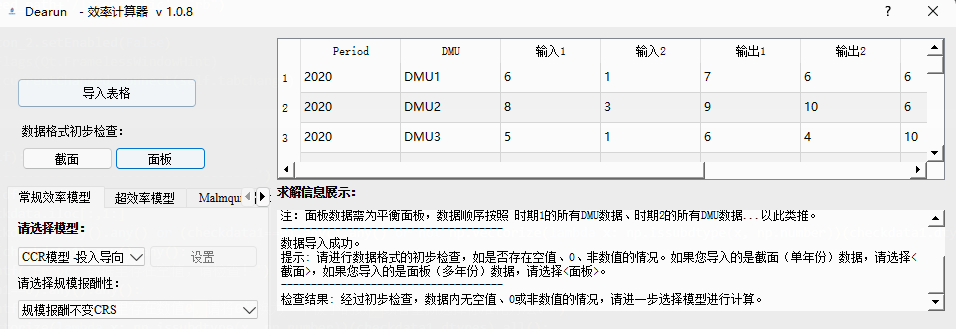
- 如数据存在上述情况,则有如下输出:
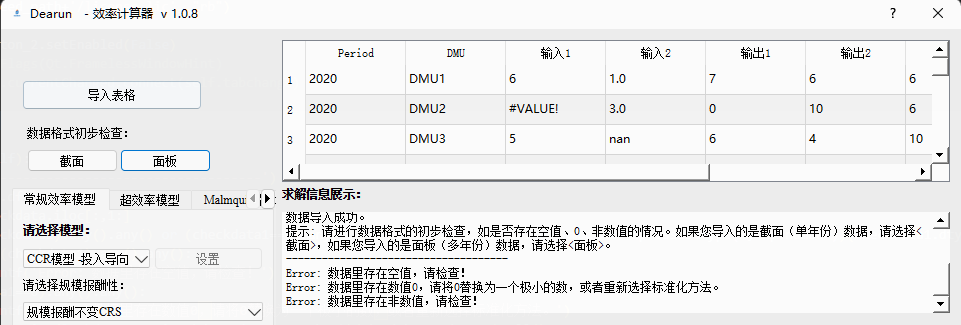
数据检查选项只会对数据进行初步的检查,没有问题不代表数据格式完全正确,请先保证您的数据是严格按照所需格式进行导入。模型选择及计算
- 正确导入表格后,会在右边栏出现表格内容
- 选择需要测算模型,默认CCR Malmquist 指数模型 -投入导向
- 选择规模报酬性,默认CRS
- 填写投入变量的个数,如果有2个投入,请填写阿拉伯数字“2”,不要写多余的字
- 填写产出变量的个数,同上
- 填写非期望产出变量的个数,同上,需注意无非期望产出的话,默认即可
- 填写测算期数,同上
- 点击“开始计算”,右边栏出现计算过程信息
- 最下面出现计算结果的表格,点击“结果保存”,结果将会储存在与你导入数据的同一个文件夹内
操作演示
以超效率SBM Malmquist指数-全局参比为例,数据同上,3个时期,包含2个投入,3个期望产出,2个非期望产出:
网络DEA模型
- 点击“导入表格”(网络dea实例数据),请注意表格的导入形式为:
DMU名称 投入 中间产品 产出 DMU1 xxx xxx xxx … … … … DMUn xxx xxx xxx
模型选择及计算
- 正确导入表格后,会在右边栏出现表格内容
- 选择需要测算模型,默认两阶段网络模型(Kao and Hwang, 2008)
- 选择规模报酬性,默认CRS
- 投入、中间产品、产出变量个数的填写同上
- 点击设置,选择在求出整体效率值后,最大化哪一阶段的效率值(0或1),默认第一阶段(详情解释请看下文)
- 计算出结果后,请点击“结果保存”
以两阶段网络模型(Kao and Hwang, 2008)为例,数据同上,包含2个投入,2个中间产品,2个产出:
视频演示
数据包络分析(DEA)方法介绍及各类模型(含非期望产出)的计算方法详解及软件实现
注:上面视频里的面板数据格式为老旧格式,请参照下面这个视频的数据格式
超详细的Malmquist、Malmquist-Luenberger指数(相邻、全局参比)处理DEA面板数据的公式与计算方法介绍
基于Excel深入理解全局Malmquist指数的计算公式与方法
模型简要介绍(必看)
交叉效率介绍
- 交叉效率的计算均基于CCR模型,
Dearun分别预设了四种交叉效率模型:
- 基础交叉效率模型
- Minimizing total deviation from the ideal point
- Minimizing the maximum d-efficiency score
- Minimizing the mean absolute deviation
- 模型1为最基础的交叉效率模型,而模型(2-4)是为了解决交叉效率计算过程中,由于线性规划最优解不唯一而导致的权重向量不唯一的问题,具体论文请参照发表在“Int. J. Production Economics”上的文章“Alternative secondary goals in DEA cross-efficiency evaluation”
- 解决交叉效率结果不唯一的还有经典的 aggresive 及 benevolent策略,也可以解决交叉效率的不唯一问题。但是由于引入的两阶段模型是非线性模型,其次,在引入新的目标后可能仍存在多解,所以本软件不涉及这两种策略
- 操作注意事项
- 在选择模型
交叉效率模型后,右边的设置按钮变为可选择状态,点开后,会出现如下界面: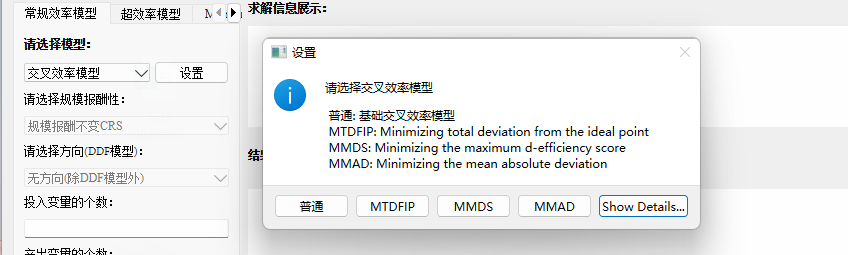
- 选择你所需要的交叉效率模型,点击一下对应的选项即可。其中MTDFIP、MMDS、MMAD均是在原有基础上引入第二阶段的目标函数,结果可能会相同,具体请参照上述提到的论文
- 上述交叉效率模型无法处理非期望指标,因为均是基于CCR模型提出,所以如果有非期望产出,请自行转为投入指标
SBM模型介绍
普通SBM模型结果解读
- 对于普通SBM模型来说,采用的是Tone2001年及2007年的文章进行建模计算(2007年定义的包含非期望产出的SBM形式)。
- 在计算结果里slack都是正的,投入slacks代表的是投入需要减少的量、产出slacks代表的是产出需要增加的量,非期望产出slacks代表的是非期望产出需要减少的量
例:对于DMU1,投入slack=1,产出slack=1,非期望产出slack=1,分别代表投入需要缩减1,产出需要扩增1,非期望产出需要缩减1,这样DMU1才是有效的
超效率SBM模型结果解读
- 对于超效率SBM模型来说,只需要对普通SBM模型里等于1的DMU代入超效率模型中进行计算,采用的是Tone2002的文章进行建模计算。
- 在计算结果里,对于小于1的,用的仍是SBM模型,slack的含义同上
- 对于大于1的,采用超效率SBM模型,为了与效率小于1的slack示以区分,slack全部标记负号,代表着超出前沿的量
例:对于DMU1,如果效率大于1,且投入slack=-1,产出slack=-1,非期望产出slack=-1,代表投入扩增1,产出缩减1,非期望产出扩增1(均为反向变化),DMU1经过这样的变化后,仍然是有效的,从而体现了一种“超”效率的思想
Directional SBM模型与Non-radial DDF模型
- Directional SBM模型与Non-radial DDF模型通过设定合适的权重或方向,两者可以相互转换,本质上是类似的模型,这里给出经典的模型定义式。
- Directional SBM模型:Fukuyama H, Weber W L. A directional slacks-based measure of technical inefficiency[J]. Socio-Economic Planning Sciences, 2010, 43(4): 274-287.
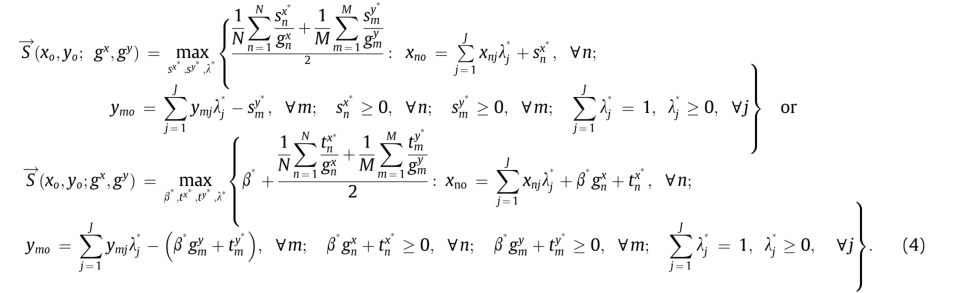
在Directional SBM模型中,采用的是论文中比较常见的方向向量,默认为
x0,y0,b0。
- Non-radial DDF模型:Barros C P, Managi S, Matousek R. The technical efficiency of the Japanese banks: Non-radial directional performance measurement with undesirable output[J]. Omega, 2012, 40: 1-8.
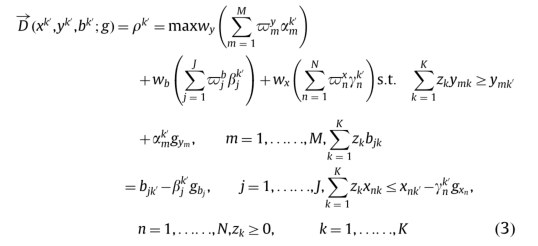
- 在Non-radial DDF模型,可自行选择方向向量,默认为
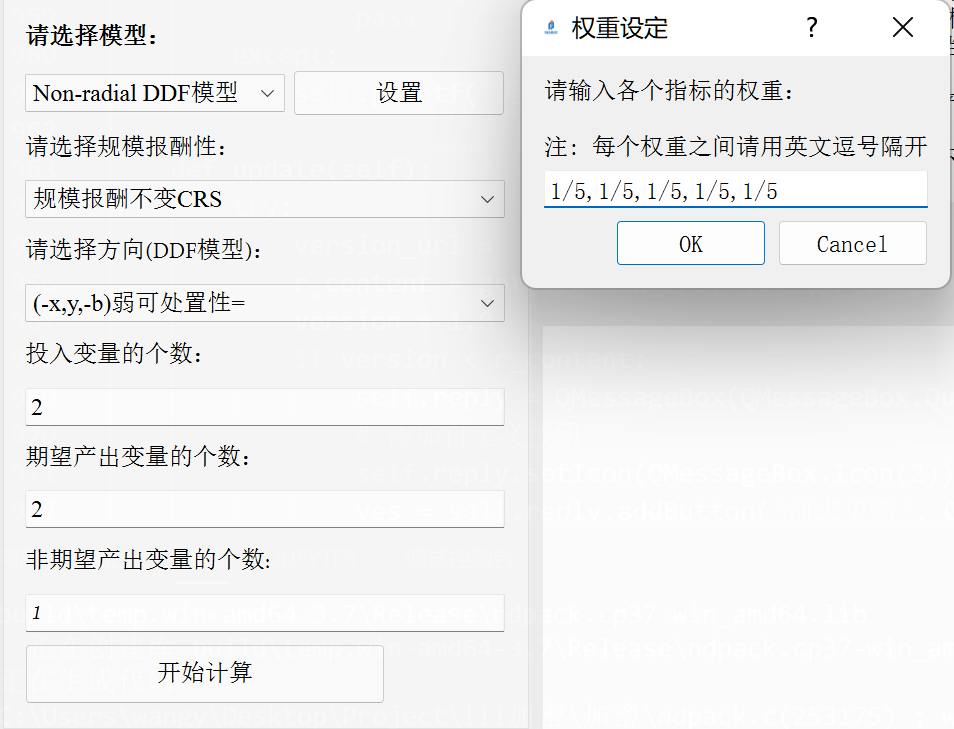
-x0,y0,-b0弱可处置性,您也可以根据选项卡设置-x0,y0,-b0强可处置性。(用的比较多的是第一种弱可处置性及第二种强可处置性形式,建议选择这两种方式) - 权重向量需要用户点击
设置选项自行指定。若指标数有n个,对应需要填写n个权重值,且权重值之前请用英文逗号,进行隔开。如有5个指标,设定相等权重值,则弹出窗口请填写1/5,1/5,1/5,1/5,1/5(如下)
EBM模型介绍
模型背景
- EBM(epsilon-based measure)模型是由Tone和Tsutsui于2010年提出的模型,融合了径向与SBM模型,将指标的改进分为了径向改进及松弛改进两部分,不同指标的处理方式不同。具体思想是通过原始数据先计算有效的投影值矩阵,并引入“affinity index”,用来定义投入/产出数据之间的“affinity matrix”,从而推导出EBM模型的两个参数
ε及w,将原始数据代入EBM模型中进行计算,从而得到最优效率值。
- 原文为Tone在2010年发表在EJOR上的文章“An epsilon-based measure of efficiency in DEA – A third pole of technical efficiency”
- 模型的引入背景及优点为:In DEA, we have two measures of technical efficiency with different characteristics: radial and non-radial. In this paper we compile them into a composite model called ‘‘epsilon-based measure (EBM).” For this purpose we introduce two parameters which connect radial and non-radial models. These two parameters are obtained from the newly defined affinity index between inputs or outputs along with principal component analysis on the affinity matrix. Thus, EBM takes into account diversity of input/output data and their relative importance for measuring technical efficiency.(摘自原文)
计算过程
- 先将所有数据通过ADD模型或SBM模型投影到有效前沿上:

- 得到投影矩阵:

- 计算所需参数:

- 代入EBM模型:
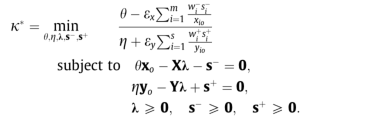
- 步骤3仅给出了对于产出系数的计算方式,投入也是一样的处理方式
- 步骤3中省略了affinity matrix的部分计算过程,具体步骤请参照原文
- 除此之外,在步骤4的模型中,加入了对θ和η的限制,分别要求θ小于等于1,η大于等于1,防止出现投入的径向改进量θ大于1的情况,产出同理
- Dearun在投影值的计算中,采用的是SBM模型
- EBM模型暂时不能处理非期望产出,如有非期望产出,请将其转为投入
结果分析
- 选项卡选择
EBM模型,设定好投入与产出,点击开始计算,求解信息展示栏会出现以下结果: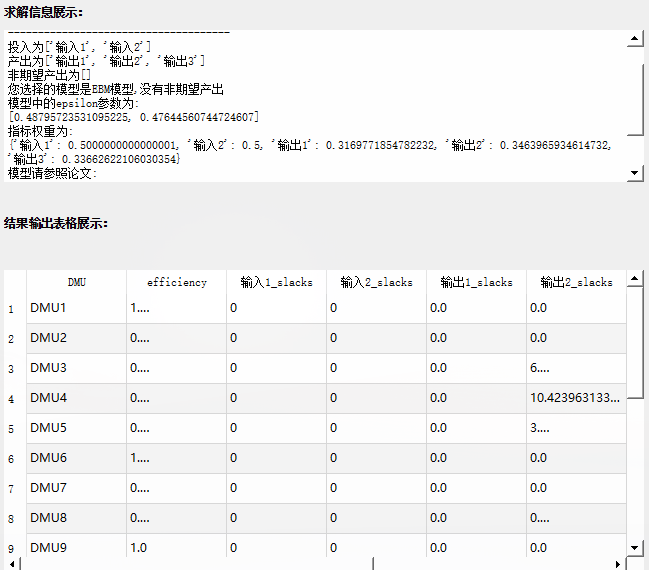
- 模型中的epsilon参数为:
[0.48795723531095225, 0.47644560744724607]分别代表投入和产出的ε值 - 指标权重为:
{'输入1': 0.5000000000000001, '输入2': 0.5, '输出1': 0.3169771854782232, '输出2': 0.3463965934614732, '输出3': 0.33662622106030354}分别代表投入、产出不同指标的权重值,并均以进行归一化处理 结果输出展示中会给出投入和产出的径向效率值及松弛改进,投入的径向改进为sita,产出的径向改进为fai
DDF模型的方向介绍
- DDF的方向及可处置性预设了以下四种:
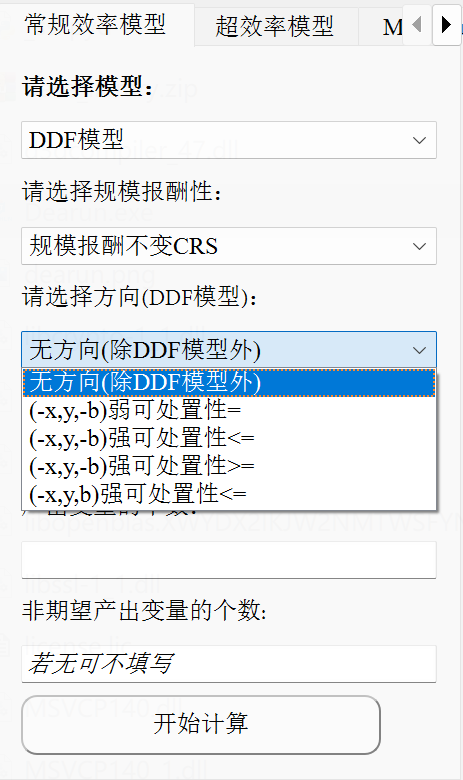
这四种方向及可处置性分别对应的非期望产出的处理方式为:
- $(-x_0,y_0,-b_0)$弱可处置性$=$: $\sum_{j=1}^{n} \lambda_{j} b_{t j} =(1-\beta) b_{t0}$
- $(-x_0,y_0,-b_0)$强可处置性$\leq$: $\sum_{j=1}^{n} \lambda_{j} b_{t j} \leq (1-\beta) b_{t0}$
- $(-x_0,y_0,-b_0)$强可处置性$\geq$: $\sum_{j=1}^{n} \lambda_{j} b_{t j} \geq (1-\beta) b_{t0}$
- $(-x_0,y_0,b_0)$强可处置性$\leq$: $\sum_{j=1}^{n} \lambda_{j} b_{t j} \leq (1+\beta) b_{t0}$
- 以上四种方向均有论文采用,具体选取什么方向请自行决定,用的比较多的是第一种弱可处置性及第二种强可处置性形式,建议选择这两种方式
注:以上四种方向中的投入及期望产出均为强可处置性
除对非期望产出的处理方式不同外,目标函数与其他约束条件均相同。
目标函数均为:
$\max \beta$
投入和期望产出的约束均为:
$\sum_{j=1}^{n} \lambda_{j} x_{i j} \leq(1-\beta) x_{i0}$
$\sum_{j=1}^{n} \lambda_{j} y_{r j} \geq(1+\beta) y_{r0}$
Malmquist模型介绍
Dearun可以求解以下几种Malmquist指数模型:
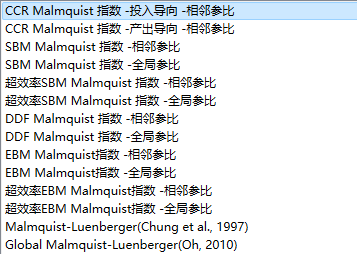
Malmquist模型结果分析
- 在表格结果中,
e-t-t+1_0代表第t+1期的DMU相比于第t期参考集的效率值$D^{t}\left(x^{t+1}, y^{t+1}, b^{t+1}\right)$,其他同理;在全局参比的结果中,e-g-t+1_0代表第t+1期的DMU相比于全局参考集的效率值$D^{G}\left(x^{t+1}, y^{t+1}, b^{t+1}\right)$,其他同理。 - 每一个时期的结果分为7列,前四列(
e-xx-xx_i的形式)均为指数的计算过程,无需关注;只需考察每个时期的后三列,effch表示效率变化,techch表示技术进步,tfpch表示TFP指数的变化率。 effch、techch、tfpch后面的数字i代表第i期的结果,如果有四年:2019,2020,2021,2022年,i=0代表2019-2020年的指数值;i=1代表2020-2021年的指数值,以此类推。
M指数、ML指数与GML指数计算方式
- ①Malmquist指数计算方式如下:
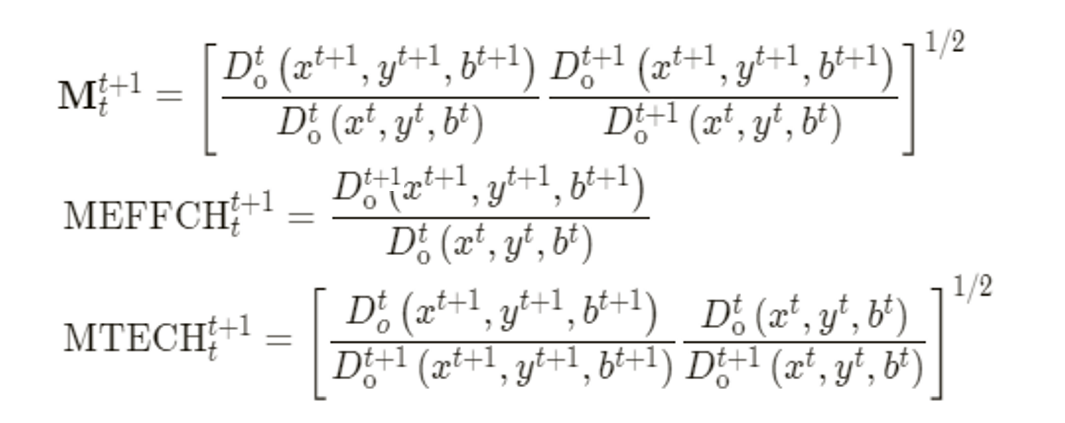
- ②全局Malmquist指数计算方式如下:
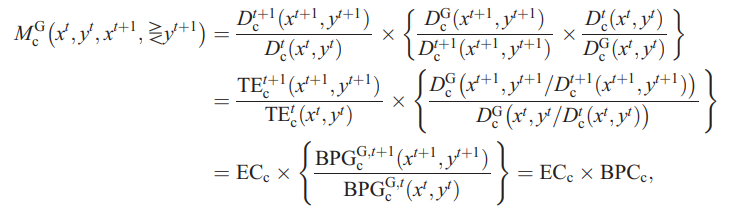
- ③Malmquist-Luenberger计算方式如下:
$$
 $$
$$ - ④Global Malmquist-Luenberger计算方式如下:
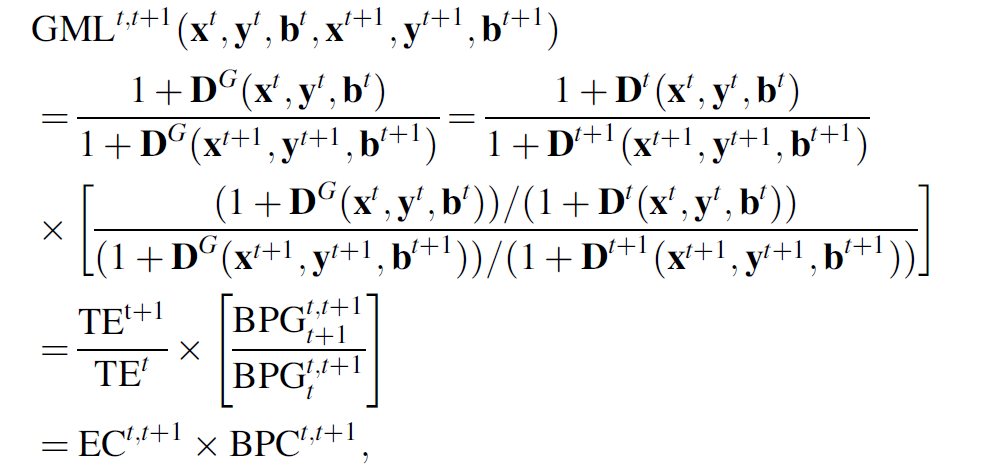
注:以上所有公式均来自原论文
- 因为用
相邻参比算跨期效率时,相当于计算超效率值,所以会出现无可行解的情况,并且VRS假设下更容易出现无可行解,读者可以先用相邻参比来计算Malmquist指数值;如果出现无可行解的情况,可以选择全局参比来计算指数。 - 基于SBM模型与SBM超效率模型的
相邻参比Malmquist指数模型一般不会出现无可行解。 EBM Malmquist指数 -相邻参比、超效率EBM Malmquist指数 -相邻参比除了会给出指数分解值外,在求解信息展示栏还会给出每一期的参数ε及w,具体定义与上一节EBM模型中的定义相同,用户可以根据需求进行保存参数EBM Malmquist指数 -全局参比、超效率EBM Malmquist指数 -全局参比除了每一期的参数ε及w外,还会给出全局的参数ε及w,用all进行表示DDF Malmquist指数 -相邻参比与DDF Malmquist指数 -全局参比中本期及跨期效率值的计算方式为$ efficiency= (1-\beta)/(1+\beta)$,之后采用公式①或②进行计算。- Malmquist-Luenberger(ML)指数模型同样是基于DDF模型的,与
DDF Malmquist指数 -相邻参比的区别是:指数的计算方式不同,ML指数模型的计算方式参考文献为:Chung et al.(1997) 的 “Productivity and undesirable outputs: A directional distance function approach”,指数计算方式为公式③。 - Global Malmquist-Luenberger(GML)指数模型同样是基于DDF模型的,与
DDF Malmquist指数 全局参比的区别是:指数的计算方式不同,GML指数模型的计算方式参考文献为:Oh(2010) 的“A global Malmquist-Luenberger productivity index”,指数计算方式为公式④。
网络DEA模型介绍
基础两阶段模型
- 目前软件加入两种经典的两阶段网络DEA模型,生产过程为:
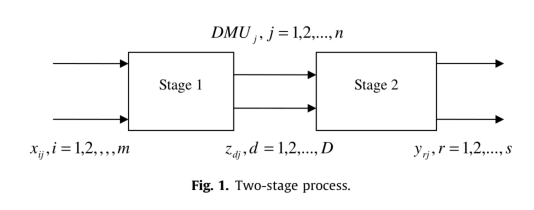
这两种模型,第一阶段的产出需全部作为第二阶段的投入
- 两个模型参考的文献分别为:
- Kao C, Hwang S N. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan[J]. European Journal of Operational Research, 2008, 185(1): 418-429.
- Yao C, Cook W D, Ning L, et al. Additive efficiency decomposition in two-stage DEA[J]. European Journal of Operational Research, 2009, 196(3): 1170-1176.
- 两个模型的区别主要是:整体效率和两个子阶段效率之间的关系分别是multiplicative和additive的,且Kao and Hwang(2008)的模型只支持CRS约束下的计算,而Yao et al.(2009)在CRS和VRS假设下均可以计算,具体模型形式请大家参考原文(如下给出了Yao et al., 2009的模型形式)。

- 前文在网络DEA操作介绍中给的实例数据为两篇论文中原文所采用的数据,由于原文中数据的数量级过大,防止计算中出现数值问题,所以对所有指标下的数据同除以了10000,结果仍然与原文是相同的。
[第一弹]网络DEA模型发展及经典模型的解读与计算(共享投入、两阶段网络DEA)
进阶两阶段模型
-
共享投入两阶段模型
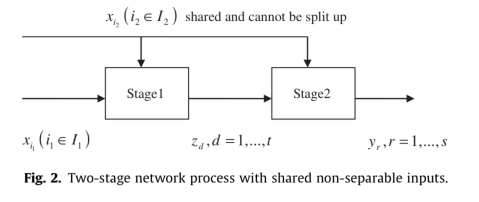
-
Centralized两阶段模型
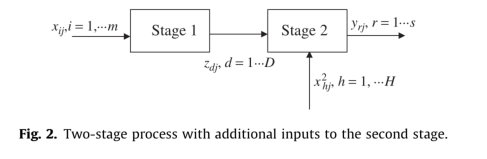
参考文献- 两个模型参考的文献分别为:
[第二弹]网络DEA模型发展及经典模型的解读与计算(共享投入、两阶段网络DEA) -
共享投入两阶段模型需要设置每个共享投入在第一阶段的比例范围,详情请参照教程视频。
-
后期将支持更多的网络DEA模型,尽请期待。
Dearun注意事项
请逐条仔细阅读下列注意事项
- 如果数据表格导入有误,将会出现
Error:数据读取有误,请检查数据的字样,那么请您重新检查数据格式 - 一定要注意数据 的正确格式,在静态模型中,第一列放DMU名称,第二列开始按照投入、产出、非期望产出的顺序放置数据,在动态模型中,第一列放时期,第二列开始按照DMU名称、投入、产出、非期望产出的顺序放置数据,确保数据准确无误,否则计算结果将出错
- 请注意指标里不能出现负数据、0数据,如果出现上列数据,请自行进行处理为正数据,本软件不内置处理方法
- 数据正常导入后,点击
开始计算后若出现出错,请检查步骤是否正确,那么请您检查是否按照上述步骤进行操作 - 在导入数据后,您可以多次测算模型,并通过最下方查看计算的结果
- 在使用CCR模型处理非期望产出指标时,会默认将非期望产出归于投入指标来进行计算(在基础CCR、超效率CCR,Malmquist CCR均采用这样的处理方式)
- CCR的CRS与VRS假设下均会给出技术效率、纯技术效率、规模效率及规模报酬情况,但是需要注意松弛改进量是不同的,与您选择的假设有关
- 请注意使用涉及到DDF的相关模型时必须选取方向,如果不选取方向将无法进行求解
- SBM与EBM模型软件内置的均为非导向,没有投入/产出导向的SBM、EBM,因为使用情况特别少
- 如在使用除DDF的模型外,方向选择一栏将变灰
- 只有选择交叉效率模型,
设置选项才可以进行选取,默认普通交叉效率 - 在使用
Malmquist模型时务必正确填写期数,如果不填写期数将无法进行求解 - 使用超效率模型时或使用VRS假设时,会由于模型不可行的问题导致无法产生最优解,会在表格里进行标注
infeasible,并会在信息框中提示您。如果出现了无可行解,建议您更换规模报酬假设、更换方向或更换模型 - 数据量纲不能差距太大,如出现量纲差距很大,请先调整量纲,否则结果可能会出错
- 由于精度问题,结果会出现0.9999999999或者1.000000000001这类型的数据,这些都视为效率等于1
- 如果您需要保存数据,请务必按下“结果保存”键,否则不会对结果进行保存
- 用到的所有模型均是基于原始论文继续复现
- 软件提供了检查更新的功能,运行后可以点击右下角的
检查更新,如果有新版本,将会提醒您去官网安装新版本 - 如果出现点击“结果保存”键没反应的情况,可能是您之前保存过同样的模型结果,且excel文件保持打开的状态,如果继续保存会生成同名文件,因此无法继续覆盖保存,所以会出现保存失败的情况。如果您遇到这种情况,请将之前的模型结果文件关闭,并修改文件名(如加入后缀等),然后再点击“结果保存”键。
- 如果您在使用中出现了什么问题,请及时联系我的邮件,也欢迎您对后续的功能进行建议
- 解释权归作者所有
 DEARUN官方网站
DEARUN官方网站